管综初数在管理类联考中占据了重要地位,无论是分数上,还是考题分布上。初数考点多、公式多、题量大以及时间紧的特点,使得在最后的冲刺阶段,很多考生都会出现忧虑、消极的心态。不知道该如何针对性的复习成为一大问题,重难点的把握不到位,在一个知识点上耗费大量时间很不值得。那就需要我们针对管综初数大纲做一个针对性的考点分析整理。
一、算术
(一)历年考题考查分布情况
历年考题算数部分考查分布情况
| 年份 |
2018 |
2017 |
2016 |
2015 |
2014 |
2013 |
2012 |
2011 |
平均比例 |
| 算术 |
3 |
3 |
1 |
3 |
2 |
2 |
1 |
1 |
8.0% |
| 考试难度 |
★ |
(二)考点整理
| 模块 |
考点 |
| 整数 |
整数及其运算 |
1.有理数无理数的性质; 2.无理数运算(分母有理化); |
| 整除、公倍数、公约数 |
1.整除、带余除法;2.最大公约数、最小公倍数性质;3. 最大公约数、最小公倍数计算方法(短除法、质因数分解法) |
| 奇数、偶数 |
运算性质:奇偶数判断、不定方程求解 |
| 质数、合数 |
定义、性质(解题突破口:2是唯一的偶质数) |
| 分数、小数、百分数 |
三者转化运算 |
| 比与比例 |
1.定义;2..比例性质:更比定理、倍比定理、反比定理、等比定理(常考:注意成立情况); |
| 数轴与绝对值 |
性质 |
对称性、非负性(非负定零)、基本不等式、三角不等式 |
| 几何意义 |
数轴表达的含义 |
| 函数图像 |
1.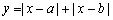 函数图像、最值 函数图像、最值
2.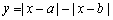 函数图像、最值 函数图像、最值 |
(三)总结
算术部分较基础,出题方式灵活多变。单独考察题目的知识点常见的有质数、奇偶数等,更多应用于综合出题,考查分值为8%左右。
二、代数
(一)历年考题考查分布情况
代数历年考查分布表
| 年份 |
2018年 |
2017年 |
2016年 |
2015年 |
2014年 |
2013年 |
2012年 |
| 题量 |
6 |
6 |
7 |
8 |
6 |
8 |
6 |
| 分值 |
18 |
18 |
21 |
24 |
18 |
24 |
18 |
| 难度 |
★★★★ |
(二)考点整理
| 模块 |
考点 |
| 整式 |
整式运算(乘法、除法) |
1.加减乘法:合并同类项; 2.除法:长除法(逐项相消); |
| 因式与因式分解 |
1.常用公式;2.十字相乘、双十字相乘; |
| 余式定理、因式定理 |
解决整式除法的有利方法,掌握其运算本质 |
| 分式 |
分式运算 |
1.计算方法;2.运算性质;3.分式裂项:适用对象、如何裂项;4.正负幂次对称分式:奇次幂、偶次幂计算方法 |
| 函数 |
集合 |
1.定义;2.元素特征:确定性、无序性、互异性;3.表示方法:区间表示法、Venn图4.集合运算:交集、并集 |
| 一元二次函数及其图像 |
1.函数表达式: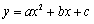 ,注意 ,注意 的取值;2.函数性质:图像、单调性、最值、对称轴、奇偶性(偶函数:b=0); 的取值;2.函数性质:图像、单调性、最值、对称轴、奇偶性(偶函数:b=0); |
| 指数函数、对数函数 |
1.指对数运算;2.函数性质:图像、单调性、过定点;3.综合:比较大小(利用特殊值、单调性以及图像判断); |
| 代数方程 |
一元一次方程 |
解得情况:例:有解,则 |
| 一元二次方程 |
1.求解方法:公式法、十字相乘;2.根的判别式;3.韦达定理的应用;4.根的分布 |
| 二元一次方程组 |
1.解的情况;2.求解方法:代入消元法、加减消元法; |
| 不等式 |
不等式性质 |
同向可加性、同向可乘性 |
| 均值不等式 |
1.适用条件:一正、二定、三相等;2.计算:和定(积有最大值)、积定(和有最小值)3.等号成立条件; |
| 不等式求解 |
1.一元二次不等式:恒成立、解集;2.分式不等式、无理不等式:求解方法;3.绝对值不等式:去绝对值是关键;4.高次不等式:穿根法(注意最高次幂正负情况、遇偶则返); |
| 数列、等差数列、等比数列 |
1.等差等比数列的定义、性质;2.通项公式、求和公式;3.最值情况; |
(三)总结
代数部分的知识点涵盖了整张考卷,基本应用于每题当中。可以单独考察得题目的知识点有很多,例如正负幂次对称分式、一元二次函数(方程、不等式)等等。。
三、几何
(一)历年考题考查分布情况
几何历年考查分布表
| 年份 |
2018年 |
2017年 |
2016年 |
2015年 |
2014年 |
2013年 |
2012年 |
| 题量 |
6 |
7 |
8 |
7 |
8 |
5 |
7 |
| 分值 |
18 |
21 |
24 |
21 |
24 |
15 |
21 |
| 所占比例 |
24% |
28% |
32% |
28% |
32% |
20% |
28% |
(二)考点整理
| 模块 |
考点 |
| 平面图形 |
三角形 |
1.五线四心; 2.面积公式;3.相似三角形的性质 |
| 四边形 |
1.面积计算公式;2.特殊四边形判别;3. 蝴蝶定理 |
| 圆与扇形 |
1.周长(弧长)、面积计算公式;2.阴影部分面积 |
| 空间几何体 |
长方体 |
1.体积、表面积计算公式;2.体对角线计算; |
| 柱体 |
1.体积、表面积计算公式;2.侧面展开图的相应计算; |
| 球体 |
1.体积、表面积计算公式;2.内接体、外接体体积、表面积计算; |
| 平面解析几何 |
平面直角坐标系 |
1.斜率;2.点的表示 |
| 直线方程与圆的方程 |
1.方程的表达式;2.位置关系:线与线、线与圆;3.对称点(线); |
| 两点间距离公式与点到直线的距离公式 |
1.两点间距离公式;2.点到直线距离公式; |
(三)总结
几何部分整体难度不大,分值却不少,需要掌握各个类型的考查题型以及相关计算公式,这样才能去解题。
四、数据分析
(一)历年考题考查分布情况
近5年考题中数据分析部分的题量统计
| 年份 |
2018 |
2017 |
2016 |
2015 |
2014 |
| 题量 |
6 |
5 |
5 |
4 |
5 |
| 分值 |
18分 |
15分 |
15分 |
12分 |
15分 |
(二)考点整理
| 模块 |
考点 |
| 计数原理 |
加法原理、
乘法原理 |
1. 加法原理、乘法原理的原理应用(分类加、分布乘); 2.涂色问题;3.做题中注意分类和分布的前后顺序; |
| 排列与排列数 |
1.排列的定义(计顺序);2.排列数公式及其应用 |
| 组合与组合数 |
1.组合的定义(不计顺序);2.组合数的公式及其应用;3.二项式定理 |
| 数据描述 |
平均值 |
计算公式 |
| 方差与标准差 |
1.计算公式(注意方差的两种计算方式);2.表示含义(离散程度) |
数据的图表
表示 |
直线分布图、扇形图等的识别计算; |
| 概率 |
事件及其简单计算 |
典型计数问题:排列、分组(分配问题中相同元素、不同元素问题)、错排(记住简单的错排方法数) |
| 加法公式 |
公式的掌握 |
| 乘法公式 |
公式的掌握 |
| 古典概型 |
公式:主要整体和要求解的部分; |
| 伯努利概型 |
公式:在做题中,审清题意、套用公式; |
(三)总结
数据分析部分出题方式灵活多变,也是在考试中最容易拉开分数的一部分。在考试中的出题偏向于基础,考生应该专注于基本的知识点和公式,不要执着于难题的计算。
免责声明:本站所提供的内容均来源于网友提供或网络搜集,由本站编辑整理,仅供个人研究、交流学习使用,不涉及商业盈利目的。如涉及版权问题,请联系本站管理员予以更改或删除
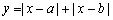 函数图像、最值
函数图像、最值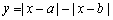 函数图像、最值
函数图像、最值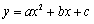 ,注意
,注意